网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设某种元件的使用寿命X的概率密度为
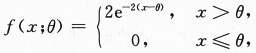
其中θ>0为未知参数.又设x1,x2,…,xn是X的一组样本观测值,求参数θ的最大似然估计值.
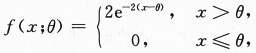
其中θ>0为未知参数.又设x1,x2,…,xn是X的一组样本观测值,求参数θ的最大似然估计值.
参考答案
参考解析
解析:

更多 “设某种元件的使用寿命X的概率密度为 其中θ>0为未知参数.又设x1,x2,…,xn是X的一组样本观测值,求参数θ的最大似然估计值.” 相关考题
考题
某种元件使用寿命X~N(μ,10^2).按照客户要求该元件使用寿命不能低于1000h,现从该批产品中随机抽取25件,其平均使用寿命为x=995,在显著性水平α=0.05下确定该批产品是否合格?
考题
设f1(x)为标准正态分布的概率密度,f2(x)为[-1,3]上均匀分布的概率密度,若为概率密度,则a,b应满足 A.A2a+3b=4
B.3a+2b=4
C.a+b=1
D.a+b=2
考题
设总体X的概率密度为其中θ∈(0,+∞)为未知参数,X1,X2,X3为来自总体X的简单随机样本,令T=max(X1,X2,X3).
(Ⅰ)求T的概率密度;
(Ⅱ)确定a,使得aT为θ的无偏估计.
考题
问答题 设X与Y相互独立,X的概率密度为 Y的概率密度为 求:(1)E(2X-3Y+1),D(2X-3Y+1); (2)Cov(X,Y),ρXY.
热门标签
最新试卷