考题
求微分方程y″+4y′= 2ex的通解.(6分)
考题
已知是线性方程组的解, 是它的导出组的解,求方程组的通解。
考题
设A=,且AX=0的基础解系含有两个线性无关的解向量,求AX=0的通解.
考题
设A为三阶矩阵,A的第一行元素为a,b,c且不全为零,又B=且AB=0,求方程组AX=0的通解.
考题
取何值时,非齐次线性方程组 (1)有唯一解 (2)无解 (3)有无穷多个解? 并在无穷多个解时,求方程组的通解。
考题
设有下列线性方程组(Ⅰ)和(Ⅱ) (Ⅰ) (Ⅱ) (1) 求方程组(Ⅰ)的通解; (2) 当方程组(Ⅱ)中的参数m,n,t为何值时,(Ⅰ)与(Ⅱ)同解?
考题
已知非齐次线性方程组 有3个线性无关的解. (Ⅰ)证明方程组系数矩阵A的秩; (Ⅱ)求的值及方程组的通解
考题
问取何值时 非齐次线性方程组, (1)有唯一解 (2)无解 (3)有无穷多个解,并在无穷多个解时,求方程组的通解
考题
设矩阵且方程组无解, (Ⅰ)求a的值; (Ⅱ) 求方程组的通解
考题
设(Ⅰ)和(Ⅱ)都是3元非齐次方程组,(Ⅰ)有通解;(Ⅱ)有通解。求(Ⅰ)和(Ⅱ) 的公共解
考题
设3阶矩阵A=[α1,α2,α3]有3个不同的特征值,且a3=a1+2a2.
(Ⅰ)证明r(A)=2;
(Ⅱ)若β=α1,α2,α3,求方程组Ax=β的通解.
考题
已知微分方程y’+y=f(x),其中f(x)是R上的连续函数.
(Ⅰ)若f(x)=x,求方程的通解.
(Ⅱ)若f(x)是周期为T的函数,证明:方程存在唯一的以T为周期的解.
考题
设,.
已知线性方程组Ax=b存在2个不同的解.
(Ⅰ)求λ,a;
(Ⅱ)求方程组Ax=b的通解.
考题
设n元线性方程组Ax=b,其中
.
(Ⅰ)证明行列式|A|=(n+1)a^n;
(Ⅱ)当a为何值时,该方程组有唯一解,并求x1;
(Ⅲ)当a为何值时,该方程组有无穷多解,并求通解.
考题
求微分方程y"-3y'+2y=2xe^x的通解.
考题
(1)求|A|;
(2)已知线性方程组AX=b有无穷多解,求a,并求A=b的通解。
考题
设(1)求lAl;
(2)已知线性方程组AX-b有无穷多解,求a,并求AX=b的通解。
考题
问答题求x3y‴+x2y″-4xy′=3x2的通解。
考题
单选题湖湘数学的主要成就有贾亨()的和丁取忠为代表的长沙数学学派。A
《数学九章》B
《数学拾遗》C
《求一术通解》D
《算法全能集》
考题
问答题设微分方程由通解y=(C1+C2x+x-1)e-x,求此微分方程。
考题
问答题微分方程y″+ay′+by=cex的一个特解为y=e2x+(1+x)ex,求a,b,c及方程的通解。
考题
问答题设y1=x,y2=x+e2x,y3=x(1+e2x)是二阶常系数线性非齐次方程的特解,求该方程及其通解。
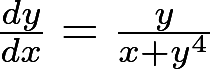 的通解
的通解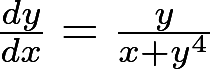 的通解
的通解
