网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
要使齐次线性方程组
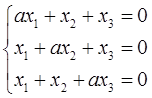
有非零解,则a应满足( )。
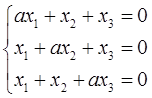
有非零解,则a应满足( )。
A. -2<a<1
B. a=1或a=-2
C. a≠-1且a≠-2
D. a>1
B. a=1或a=-2
C. a≠-1且a≠-2
D. a>1
参考答案
参考解析
解析:齐次线性方程组的系数矩阵作初等变换如下
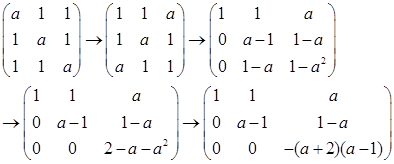
要使齐次线性方程组有非零解,则矩阵的秩r<3,因此得a-1=0或-(a+2)(a-1)=0,计算得a=1或a=-2。
【说明】n元齐次线性方程组Ax=0有非零解的充要条件是r(A)<n。
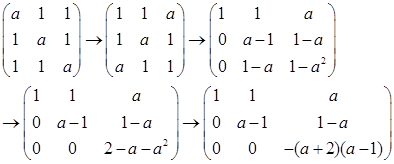
要使齐次线性方程组有非零解,则矩阵的秩r<3,因此得a-1=0或-(a+2)(a-1)=0,计算得a=1或a=-2。
【说明】n元齐次线性方程组Ax=0有非零解的充要条件是r(A)<n。
更多 “要使齐次线性方程组 有非零解,则a应满足( )。 A. -2<a<1 B. a=1或a=-2 C. a≠-1且a≠-2 D. a>1 ” 相关考题
考题
设Ax=b是一非齐次线性方程组,η1,η2是其任意2个解,则下列结论错误的是()
A、η1+η2是Ax=0的一个解B、(1/2)η1+(1/2)η2是Ax=b的一个解C、η1-η2是Ax=0的一个解D、2η1-η2是Ax=b的一个解
考题
设A是m×n阶矩阵,Ax=0是非齐次线性方程组Ax=b所对应的齐次线性方程组,则下列结论正确的是( )。A.若Ax=0仅有零解,则Ax=b有惟一解
B.若Ax=0有非零解,则Ax=b有无穷多个解
C.若Ax=b有无穷多个解,则Ax=0仅有零解
D.若Ax=b有无穷多个解,则Ax=0有非零解
考题
设n阶矩阵A的伴随矩阵A^*≠0,若ζ1,ζ2,ζ3,ζ4是非齐次线性方程组Ax=b的互不相等的解,则对应的齐次线性方程组Ax=0的基础解系A.不存在.
B.仅含一个非零解向量.
C.含有两个线性无关的解向量.
D.含有三个线性无关的解向量.
考题
设A是4×5矩阵,ξ1,ξ2是齐次线性方程组Ax=0的基础解系,则下列结论正确的是( ).A.ξ1-ξ2,ξ1+2ξ2也是Ax=0的基础解系
B.k1ξ1+k1ξ2是Ax=0的通解
C.k1ξ1+ξ2是Ax=0的通解
D.ξ1-ξ2,ξ2-ξ1也是Ax=0的基础解系
考题
已知4元非齐次线性方程组Ax=b的系数矩阵的秩等于3,且η1,η2,η3是3个不同的解向量,则通解是( ).A.x=k1(η-η2)+η3
B.x=k1η1+k2η2+η3
C.x=k1η1+k2η2+k3η3
D.x=k1(η+η2)+η3
考题
齐次线性方程组的基础解系为()。A、α1=(1,1,1,0)T,α2=(-1,-1,1,0)TB、α1=(2,1,0,1)T,α2=(-1,-1,0)TC、α1=(1,1,1,0)T,α2=(1,0,0,1)TD、α1=(2,1,0,1)T,α2=(-2,-1,0,1)T
考题
填空题已知四元非齐次方程组AX(→)=b(→),r(A)=3,α(→)1,α(→)2,α(→)3是它的三个解向量,且α(→)1+α(→)2=(1,1,0,2)T,α(→)2+α(→)3=(l,0,1,3)T,则AX(→)=b(→)的通解是____。
考题
单选题设函数y1(x)、y2(x)、y3(x)线性无关,且都是二阶非齐次线性方程y″+p(x)y′+q(x)y=f(x)的解,又c1与c2为任意常数,则该非齐次线性方程的通解可表示为( )。A
c1y1+c2y2+y3B
c1y1+c2y2-(c2+c1)y3C
c1y1+c2y2-(1-c1-c2)y3D
c1y1+c2y2+(1-c1-c2)y3
考题
单选题设n元齐次线性方程组AX(→)=0(→),秩(A)=n-3,且α(→)1,α(→)2,α(→)3为其3个线性无关的解,则( )为其基础解系。A
α(→)1+α(→)2,α(→)2+α(→)3,α(→)1+α(→)3B
α(→)1-α(→)2,α(→)2-α(→)3,α(→)3-α(→)1C
α(→)1+α(→)2+α(→)3,α(→)3-α(→)2,α(→)1+2α(→)3D
α(→)1-α(→)2,2α(→)2-3α(→)3,3α(→)3-2α(→)1
考题
单选题已知β(→)1β(→)2是非齐次方程组AX(→)=b(→)的两个不同的解,α(→)1α(→)2是其对应的齐次线性方程组的基础解系,k1、k2是任意常数,则方程组AX(→)=b(→)的通解必是( )。A
k1α(→)1+k2(α(→)1+α(→)2)+(β(→)1-β(→)2)/2B
k1α(→)1+k2(α(→)1-α(→)2)+(β(→)1+β(→)2)/2C
k1α(→)1+k2(β(→)1+β(→)2)+(β(→)1-β(→)2)/2D
k1α(→)1+k2(β(→)1-β(→)2)+(β(→)1+β(→)2)/2
考题
单选题齐次线性方程组的基础解系为()。A
α1=(1,1,1,0)T,α2=(-1,-1,1,0)TB
α1=(2,1,0,1)T,α2=(-1,-1,0)TC
α1=(1,1,1,0)T,α2=(1,0,0,1)TD
α1=(2,1,0,1)T,α2=(-2,-1,0,1)T
考题
单选题已知n元非齐次线性方程组Ax=B,秩r(A)=n-2,α1,α2,α3为其线性无关的解向量,k1,k2为任意常数,则Ax=B的通解为( )。[2014年真题]A
x=k1(α1-α2)+k2(α1+α3)+α1B
x=k1(α1-α3)+k2(α2+α3)+α1C
x=k1(α2-α1)+k2(α2-α3)+α1D
x=k1(α2-α3)+k2(α1+α2)+α1
考题
单选题已知非齐次线性方程组有无限多个解,则t等于().A
-1B
1C
4D
-1或4
热门标签
最新试卷