考题
设三阶矩阵A的特征值为1,1,2,则2A+E的特征值为()。
A、3,5B、1,2C、1,1,2D、3,3,5
考题
设A为三阶方阵,其特征值为1,-1,2,则A^2的特征值为1,1,4。()
此题为判断题(对,错)。
考题
设 2 是方阵 A 的特征值,则必有特征值
A.0
B.1
C.-1
D.以上都不对
考题
设是非奇异矩阵A的特征值,则矩阵(2A3)- 1有一个特征值为:
A.3
B.4
C.
D.1
考题
设λ=1/2是非奇异矩阵A的特征值,则矩阵(2A3)-1有一个特征值为:
A. 3 B.4 C.1/4 D. 1
考题
设二次型. (Ⅰ)求二次型的矩阵的所有特征值; (Ⅱ)若二次型的规范形为,求的值
考题
设3阶实对称矩阵A的特征值为-1,1,1,与特征值-1对应的特征向量x=(-1,1,1)′,求A
考题
设A为三阶实对称矩阵,A的每行元素之和为5,AX=0有非零解且λ1=2是A的特征值,
对应特征向量为(-1,0,1)^T.
(1)求A的其他特征值与特征向量;
(2)求A.
考题
已知二次型可用正交变换化为.求a,并且作实现此转化的正交变换
考题
设实对称阵A的特征值为0,2,2,且对应特征值2的两个特征向量为与,求.
考题
设二次型
(b>0),
其中二次型的矩阵A的特征值之和为1,特征值之积为-12.
(1)求a,b的值;
(2)利用正交变换将二次型f化为标准形,并写出所用的正交变换和对应的正交矩阵.
考题
已知二次型的秩为2.(1)求a.(2)求作正交变换X=QY,把f(x1,x2,x3)化为标准形.(3)求方程f(x1,x2,x3)=0的解
考题
已知二次型经过正交变换化为标准型,求参数a,b及所用的正交变换矩阵
考题
设二次型,(b>0)其中A的特征值之和为1, 特征值之积为-12.(1) 求a,b. (2) 用正交变换化为标准型
考题
二次型, (1)求f(x1,x2,x3)的矩阵的特征值. (2)设f(x1,x2,x3)的规范形为. 求a
考题
设A是三阶实对称矩阵,r(A)=1,A^2-3A=O,设(1,1,-1)t为A的非零特征值对应的特征向量.(1)求A的特征值;(2)求矩阵A.
考题
设二次型其中二次型矩阵A的特征值之和为1, 特征值之积-12.(1) 求a,b的值; (2) 求一正交变换把二次型化成标准型(需写出正交变换及标准型)
考题
设二次型f(x1,x2,x3)=(a>0)的秩为2.(1)求a;(2)用正交变换法化二次型为标准形.
考题
已知,二次型的秩为2. (Ⅰ)求实数a的值; (Ⅱ)求正交变换将二次型化为标准型
考题
设矩阵A=
(1)已知A的一个特征值为3,试求y;
(2)求可逆矩阵P,使(AP)^T(AP)为对角矩阵.
考题
设A为二阶矩阵,α1,α2为线性无关的二维列向量,Aα1=0,Aα2=2α1+α2,则A的非零特征值为________.
考题
设A为三阶实对称矩阵,如果二次曲面方程
在正交变换下的标准方程的图形如图所示,
则A的正特征值的个数为 A.A0
B.1
C.2
D.3
考题
设二次型的正惯性指数p=2,负惯性指数q=0,且可用可逆线性变换x=Cy将其化为二次型(1)求常数a; (2)求可逆线性变换矩阵C
考题
三阶矩阵 为矩阵A的转置,已知r(ATA)=2,且二次型
(1)求a;
(2)求二次型对应的二次矩阵,并将二次型化为标准型,写出正交变换过程。
考题
设二次型f(x1,x2,x3)在正交变换为x=py下的标准形为
若Q=(e1-e3,e2),则f(x1,x2,x3)在正交变换x=Qy下的标准型为( )。
A.
B.
C.
D.
考题
单选题设A是三阶矩阵,α1=(1,0,1)T,α2=(1,1,0)T是A的属于特征值1的特征向量,α3=(0,1,2)T是A的属于特征值-1的特征向量,则:()A
α1-α2是A的属于特征值1的特征向量B
α1-α3是A的属于特征值1的特征向量C
α1-α3是A的属于特征值2的特征向量D
α1+α2+α3是A的属于特征值1的特征向量

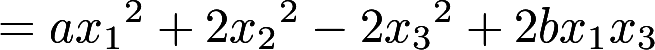 ,(b>0)其中A的特征值之和为1, 特征值之积为-12.(1) 求a,b. (2) 用正交变换化
,(b>0)其中A的特征值之和为1, 特征值之积为-12.(1) 求a,b. (2) 用正交变换化 为标准型
为标准型
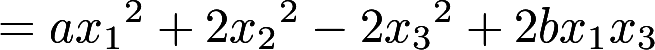 ,(b>0)其中A的特征值之和为1, 特征值之积为-12.(1) 求a,b. (2) 用正交变换化
,(b>0)其中A的特征值之和为1, 特征值之积为-12.(1) 求a,b. (2) 用正交变换化 为标准型
为标准型


