网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
设矩阵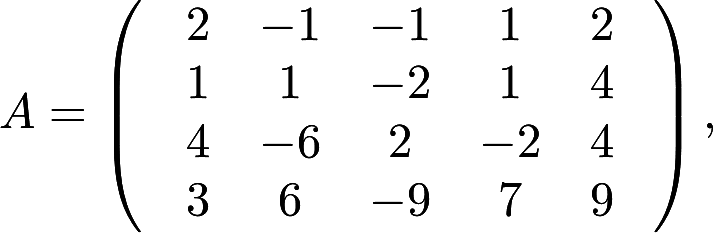
求矩阵A的列向量组的一个极大无关组, 并把不属于极大无关组的列向量用极大无关组线性表示出来.
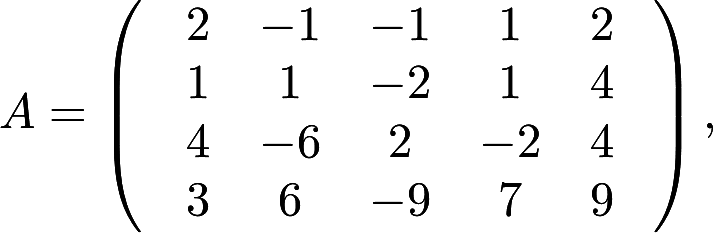求矩阵A的列向量组的一个极大无关组, 并把不属于极大无关组的列向量用极大无关组线性表示出来.参考答案
参考解析
解析：
更多 “设矩阵求矩阵A的列向量组的一个极大无关组, 并把不属于极大无关组的列向量用极大无关组线性表示出来.” 相关考题
考题
设A为m×n阶矩阵，则齐次线性方程组AX=0只有零解的充分必要条件是(64)。A．A的列向量组线性无关B．A的列向量组线性相关C．A的行向量组线性无关D．A的行向量组线性相关A.A的列向量组线性无关B.A的列向量组线性相关C.A的行向量组线性无关D.A的行向量组线性相关
考题
设A，B为满足AB=0的任意两个非零矩阵，则必有(56)。A．A的列向量组线性相关，B的行向量组线性相关B．A的列向量组线性相关，B的列向量组线性相关C．A的行向量组线性相关，B的行向量组线性相关D．A的列向量组线性相关，B的列向量组线性相关
考题
设A，B，C均为n阶矩阵，若AB=C，且B可逆，则
A.A矩阵C的行向量组与矩阵A的行向量组等价
B.矩阵C的列向量组与矩阵A的列向量组等价
C.矩阵C的行向量组与矩阵B的行向量组等价
D.矩阵C的列向量组与矩阵B的列向量组等价
考题
设矩阵A,B,C均为n阶矩阵，若AB=C，且B可逆，则（ ）
A.矩阵C的行向量组与矩阵A的行向量组等价
B.矩阵C的列向量组与矩阵A的列向量组等价
C.矩阵C的行向量组与矩阵B的行向量组等价
D.矩阵C的行向量组与矩阵B的列向量组等价
考题
设A为m×n矩阵，则齐次线性方程组Ax＝0有非零解的充分必要条件是（ ）。
A、矩阵A的任意两个列向量线性相关
B、矩阵A的任意两个列向量线性无关
C、矩阵A的任一列向量是其余列向量的线性组合
D、矩阵A必有一个列向量是其余列向量的线性组合
考题
设A为4X5矩阵，且A的行向量组线性无关，则（ ）.《》（ ）A.A的列向量组线性无关
B.方程组AX=b有无穷多解
C.方程组AX=b的增广矩阵的任意四个列向量构成的向量组线性无关
D.A的任意4个列向量构成的向量组线性无关
考题
单选题设n维列向量组α1，α2，…，αm（m＜n）线性无关，则n维列向量组β1，β2，…，βm线性无关的充分必要条件是（ ）.A
向量组α1，α2，…，αm可以由β1，β2，…，βm线性表示B
向量组β1，β2，…，βm可以由α1，α2，…，αm线性表示C
向量组α1，…，αm与向量组β1，…，βm等价D
矩阵A=（α1，…，αm）与矩阵B=（β1，…，βm）β）m
考题
单选题设向量组α(→)1，α(→)2，…，α(→)r（Ⅰ）是向量组α(→)1，α(→)2，…，α(→)s（Ⅱ）的部分线性无关组，则（ ）。A
（Ⅰ）是（Ⅱ）的极大线性无关组B
r（Ⅰ）＝r（Ⅱ）C
当（Ⅰ）中的向量均可由（Ⅱ）线性表示时，r（Ⅰ）＝r（Ⅱ）D
当（Ⅱ）中的向量均可由（Ⅰ）线性表示时，r（Ⅰ）＝r（Ⅱ）
考题
单选题设A为m×n矩阵，则齐次线性方程组Ax＝0有非零解的充分必要条件是（ ）。[2017年真题]A
矩阵A的任意两个列向量线性相关B
矩阵A的任意两个列向量线性无关C
矩阵A的任一列向量是其余列向量的线性组合D
矩阵A必有一个列向量是其余列向量的线性组合
考题
单选题设A为4×5矩阵，且A的行向量组线性无关，则（ ）。A
A的列向量组线性无关B
方程组AX(→)＝b(→)有无穷多解C
方程组AX(→)＝b(→)的增广矩阵A(＿)的任意四个列向量构成的向量组线性无关D
A的任意4个列向量构成的向量组线性无关
考题
单选题设n维列向量组α(→)1，α(→)2，…，α(→)m（m＜n）线性无关，则n维列向量组β(→)1，β(→)2，…，β(→)m线性无关的充分必要条件是（ ）。A
向量组α(→)1，α(→)2，…，α(→)m可以由β(→)1，β(→)2，…，β(→)m线性表示B
向量组β(→)1，β(→)2，…，β(→)m可以由α(→)1，α(→)2，…，α(→)m线性表示C
向量组α(→)1，α(→)2，…，α(→)m与向量组β(→)1，β(→)2，…，β(→)m等价D
矩阵A＝（α(→)1，α(→)2，…，α(→)m）与矩阵B＝（β(→)1，β(→)2，…，β(→)m）等价
考题
填空题已知向量组（α(→)1，α(→)3），（α(→)1，α(→)3，α(→)4），（α(→)2，α(→)3）都线性无关，而（α(→)1，α(→)2，α(→)3，α(→)4）线性相关，则向量组（α(→)1，α(→)2，α(→)3，α(→)4）的极大无关组是____。
考题
问答题设向量组α(→)1，α(→)2，…，α(→)s的秩为r＞0，证明： （1）α(→)1，α(→)2，…，α(→)s中任意r个线性无关的向量都构成它的一个极大线性无关组； （2）若α(→)1，α(→)2，…，α(→)s中每个向量都可由其中某r个向量线性表示，则这r个向量必为α(→)1，α(→)2，…，α(→)s的一个极大线性无关组。
热门标签
最新试卷
