网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
设X1,X2,X3,X4,X5为来自正态总体X～N(0,4)的简单随机样本,y=a（X1-2X2）^2+b(3X3-4X3)^2+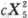
(abc≠o),且y～χ^2（n）,则a=_______,b=_______,c=_______,b=_______.
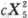(abc≠o),且y～χ^2（n）,则a=_______,b=_______,c=_______,b=_______.参考答案
参考解析
解析：因为X1-2X2～N(0，20)，3X3-4X4～N(0，100)，X5～N(0，4)，所以
于是
于是
更多 “设X1,X2,X3,X4,X5为来自正态总体X～N(0,4)的简单随机样本,y=a（X1-2X2）^2+b(3X3-4X3)^2+(abc≠o),且y～χ^2（n）,则a=_______,b=_______,c=_______,b=_______.” 相关考题
考题
设总体X～N(μ，σ2)，X1，X2，X3，X4是正态总体X的一个样本，为样本均值，S2为样本方差，若μ为未知参数且σ为已知参数，下列随机变量中属于统计量的有( )。A．X1-X2+X3B．2X3-μC．D．E．
考题
一个关系模式为Y(X1,X2,X3,X4)，假定该关系存在函数依赖：(X1,X2)→X3，X2→X4，则该关系的码为______。A．X1B．X2C．(X1，X2)D．(X1,X2,X3,X4)
考题
假设某总体服从正态分布N(12, 4)，现从中随机抽取一容量为5的样本X1,X2, X3, X4, X5，则：
概率P{max(X1,X2, X3, X4, X5) >15)=( )。
A. 0.2533 B. 0. 2893 C. 0.2923 D. 0.2934
考题
设总体X的概率密度为其中θ∈(0,+∞)为未知参数，X1，X2，X3为来自总体X的简单随机样本，令T=max(X1，X2，X3).
(Ⅰ)求T的概率密度；
(Ⅱ)确定a，使得aT为θ的无偏估计.
考题
单选题已知被测量Y与输入量X1、X2、X3、X4、X5、的估计值分别为y、x1、x2、x3、x4、x5，它们之间的函数关系为y=x1+x2+x3+x4+x5，若输入量X1、X2、X3、X4、X5服从半宽度相同的均匀分布，且相互独立，则被测量Y在相应变化区间内接近（ ）分布。A
正态B
均匀C
三角D
反正弦
热门标签
最新试卷