网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
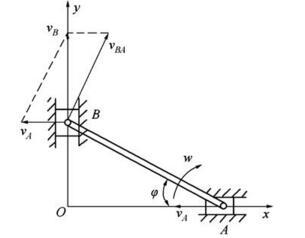
椭圆规尺的A端以速度vA沿x轴的负向运动,如图所示,AB=l。则尺AB的角速度为( )。

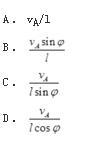
参考答案
参考解析
解析:由A、B速度方向确定AB的转动瞬心,因A点速度水平,B点速度竖直,作速度的垂线,其交点为即速度瞬心,则A点的转动半径


更多 “椭圆规尺的A端以速度vA沿x轴的负向运动,如图所示,AB=l。则尺AB的角速度为( )。 ” 相关考题
考题
刚体作平面运动,某瞬时平面图形的角速度为ω,角加速度为α,则其上任意两点A、B的加速度在A、B连线上投影的关系是:
A.比相等
B.相差AB * ω2
C.相差AB * α
D.相差(AB * ω2 + AB * α)
考题
杠OA = l ,绕定轴 O 以角速度ω 转动,同时通过 A 端推动滑块 B 沿轴 x 运动,设分析运动的时间内杆与滑块并不脱离,则滑块的速度ν B 的大小用杆的转角? 与角速度ω 表示为:
(A)ν B = lωsin ?
(B)ν B = lωcos ?
(C)ν B = lωcos2 ?
(D)ν B =lωsin2 ?
考题
杠OA=l,绕定轴O以角速度ω转动,同时通过A端推动滑块B沿轴X运动,设分析运动的时间内杆与滑块并不脱离,则滑块的速度vB的大小用杆的转角φ与角速度ω表示为:
A. vB= lωcosinφ B. vB=lωcosφ
C. vB=lωcos2φ D. vB=lωsin2φ
考题
如图。在直角梯形ABCD中,AB∥CD,∠BAD=90o,且AB=8,AD=3,CD=4,动点P,Q分别以点B和点A为起点同时出发,点P沿B→A,以每秒1个单位速度运动,终点为点A;点Q沿A→D→C→B,以每秒1.5个单位速度运动,终点为点B。设△APQ的面积为y,运动时间为x。
(1)求y关于x的函数解析式y=f(x);
(2)画出函数y=f(x)的图象。
考题
圆盘某瞬时以角速度ω,角加速度α绕O轴转动,其上A、B两点的加速度分别为aA和aB,与半径的夹角分别为θ和φ。若OA=R,OB=R/2,则aA与aB,θ与φ的关系分别为:
A.aA=aB,θ=φ
B. aA=aB,θ=2φ
C. aA=2aB,θ=φ
D. aA=2aB,θ=2φ
考题
杆OA=1,绕定轴O以角速度ω转动,同时通过A端推动滑块B沿轴x运动(图4-49)。设分析运动的时间内杆与滑块并不脱离,则滑块的速度vB的大小用杆的转角φ与角速度ω表示为( )。
A. vB=lωsinφ
B. vB=lωcosφ
C. vB=lωcos2φ
D. vB=lωsin2φ
考题
图4-49所示机构中,曲柄OA以匀角速度绕O轴转动,滚轮B沿水平面作纯滚动,如图4-48所示。己知OA=l, AB=2l,滚轮半径为r。在图示位置时,OA铅直,滚轮B的角速度为( )。
考题
如图4-45所示,圆盘某瞬时以角速度ω,角加速度α绕轴O转动,其上A、B两点的加速度分别为aA和aB,与半径的夹角分别为θ和φ。若OA=R, OB = R/2,则aA与aB,θ与 φ 的关系分别为( )。
A.aA=aB θ=φ B.aA=aB θ=2φ C.aA=2aB θ=φ D.aA=2aB θ=2φ
考题
单选题刚体作平面运动,某瞬时平面图形的角速度为w,角加速度为α,则其上任意两点A、B的加速度在A、B连线上投影的关系是:()A
比相等B
相差AB·w2C
相差AB·αD
相差(AB·w2+AB·α)
热门标签
最新试卷